Tower of Hanoi from a Math Point of View

What we'll talk about

In the previous article about the Tower of Hanoi, we explored the puzzle by examining its history and rules, and we developed an algorithm capable of solving the puzzle for any number of disks. If you haven't read it yet, click here.

This time, we'll discuss the Tower of Hanoi from a mathematical perspective, deriving a formula that represents the puzzle's solution and understanding how mathematics helps us determine the algorithm's complexity.

A solid understanding of the logic behind the puzzle is important, so ensure you're comfortable with that before proceeding.

Prerequisites

• Required: Have read the previous article about the Tower of Hanoi

Introduction

Tower of Hanoi puzzle is much more than a simple puzzle used to exercise logic, it also has a significant relationship with math.

In the previous article, we couldn't determine the complexity of the algorithm we developed to solve the puzzle. This is where mathematics can help us.

To achieve this, the first step is to find a way to represent the resolution of the problem using a mathematical formula. It might seem daunting at first, but trust me, it's not that complicated. Patience is key here; my advice is to read and re-read each part of the explanation until every concept is clear.

Recursive form

The best way to solve any problem is by generalizing it. This means broadening the scope of a specific problem to a wider context, creating a more general version that can encompass various particular cases.

That's why we'll call the number of disks in the tower as $n$.

The advantage of this approach is that we can increase or decrease the number of disks in the tower, and the formula will work without any problem.

The second step is to establish a nomenclature that will be used in the problem resolution. For this purpose we define that $T_n$ is the minimum number of moves needed to complete the tower.

So, to summarize:

• $n$ is the number of disks
• $T_n$ is the minimum number of moves needed to complete a tower with $n$ disks
  • For example, T1T_1T1​ is the minimum number of moves needed to complete a tower with 1 disk, T2T_2T2​ is for 2 disks, and so on

The next step is to identify some statements that, although obvious, will help us find patterns in the problem:

• Solving a tower with no disks takes 0 moves, so $T_0 = 0$.
• Solving a tower with 1 disk takes 1 move, so $T_1 = 1$

We already know that to solve a tower with 3 disks, we first need to complete a tower with 2 disks, then move the third disk, and finally move the other 2 disks above the third disk.

Generalizing it, to solve a tower with $n$ disks we first need to solve a tower with $n-1$ disks, move the $n$th disk and then move $n-1$ disks above the $n$th disk.

Now bringing some math, to resolve a tower with $n$ disks we first need to resolve a tower with $n-1$ disks, which costs $T_{n-1}$ moves. Then we move the $n$th disk, which takes $1$ move. Finally we move the $n-1$ tower on top of the $n$th disk, which costs another $T_{n-1}$ moves.

We can express this logic using the following mathematical formula:

$T_0 = 0$ $T_n = 2T_{n-1} + 1$

Note in the formula above that the solution of a $T_n$ depends of the solution of a $T_{n-1}$ tower, that is a recursion represented in math!

Like a recursion in coding, without a base case, it would continue indefinitely without reaching a solution. Hence, the statement T0=0T_0 = 0T0​=0 serves as the base case that stops the recursion appropriately.

Understanding the logic behind the game and creating an appropriate nomenclature helped us to describe the problem's formula in a simple way.

Closed form

So, we've found a formula that can solve the Tower of Hanoi puzzle for any number of disks, which is great. However, solving it directly using this formula can be challenging because it involves resolving each recursion step-by-step, which can be difficult. Furthermore, this recursive formula doesn't directly provide insights into the complexity of the Tower of Hanoi algorithm; it merely represents our code in a mathematical form.

What we really want is to derive a closed formula that is easy to compute and helps us determine the time complexity of solving the Tower of Hanoi.

To achieve this, let's manipulate the formula we've already established:

$T_n = 2T_{n-1} + 1$

Firstly, let's add 1 to both sides of the equation:

$T_n + 1 = 2T{n-1} + 2$

Now, let's introduce a new notation:

$T_n + 1 = U_n$

There's nothing complicated here, $U_n$ is an arbitrary notation that we've created to represent $T_n + 1$.

Replacing the values using the new notation $U_n$ we get:

$U_n = T_n + 1$ $U_n = (2T_{n-1} + 1) + 1$ $U_n = 2T_{n-1} + 2$ $U_n = 2(T_{n-1} + 1)$ $U_n = 2(U_{n-1})$, for $n > 0$

1. We introduced the new notation UnU_nUn​ in the previous step
2. We expanded $T_n$ into $2T_{n-1} + 1$, which represents the same value in a different form. If it's not clear, revisiting the recursive form might help
3. We eliminate the parentheses resolving the possible operations
4. We extracted the $2$ from $2T_{n-1}$ and $2$ and isolated it outside the parentheses
5. We replaced $T_{n-1} + 1$ with $U_{n-1}$, which is equivalent to the notation we defined earlier

The manipulations might seen difficult to grasp at first. I recommend going step by step and truly understand what's happening in each phase, don't skip steps!

Given the formulas we've established:

$U_0 = 1$ $U_n = 2(U_{n-1})$

We can derive the following sequence:

$U_n = 2(U_{n-1})$ $U_n = 2(2(U_{n-2}))$ $U_n = 2(2(2(U_{n-3})))$

Now, let's apply actual numbers:

$U_3 = 2(U_{2})$ $U_3 = 2(2(U_{1}))$ $U_3 = 2(2(2(U_{0})))$ $U_3 = 2(2(2(1)))$ $U_3 = 2 * 2 * 2$ $U_3 = 2^3$

From the statements above, we can assume that:

$U_n = 2^n$

As last step we need to go back to the $T_n$ notation, so replacing we have:

$U_n = 2^n$ $T_n + 1 = 2^n$ $T_n = 2^n - 1$

1. We derived the definition from the previous steps
2. Using the definition, we substituted $U_n$ with $T_{n-1}$
3. Finally, we subtracted 1 from both sides of the equation

Now we can find the number of steps needed to resolve the Tower of Hanoi puzzle using the closed formula $T_n = 2^n + 1$ and simply replacing $n$ with the actual number of disks in the tower.

Now, we have a closed formula $T_n = 2^n + 1$ that allows us to determine the number of steps needed to solve the Tower of Hanoi puzzle simply by substituting $n$ with the actual number of disks in the tower.

Algorithm's Complexity

Now we're closer than ever to understanding the complexity of the Tower of Hanoi algorithm, as we have derived a formula to determine the number of steps required to solve the puzzle with any number of disks.

Applying the formula in Big O notation, we get:

$O(2^n + 1)$

Since in Big O notation we always drop the constants, we find that the complexity of the Tower of Hanoi algorithm is $O(2^n)$, also known as Exponential Time.

An exponential time algorithm is a truly slow one, and that's make a lot of sense considering the mythology behind the puzzle.

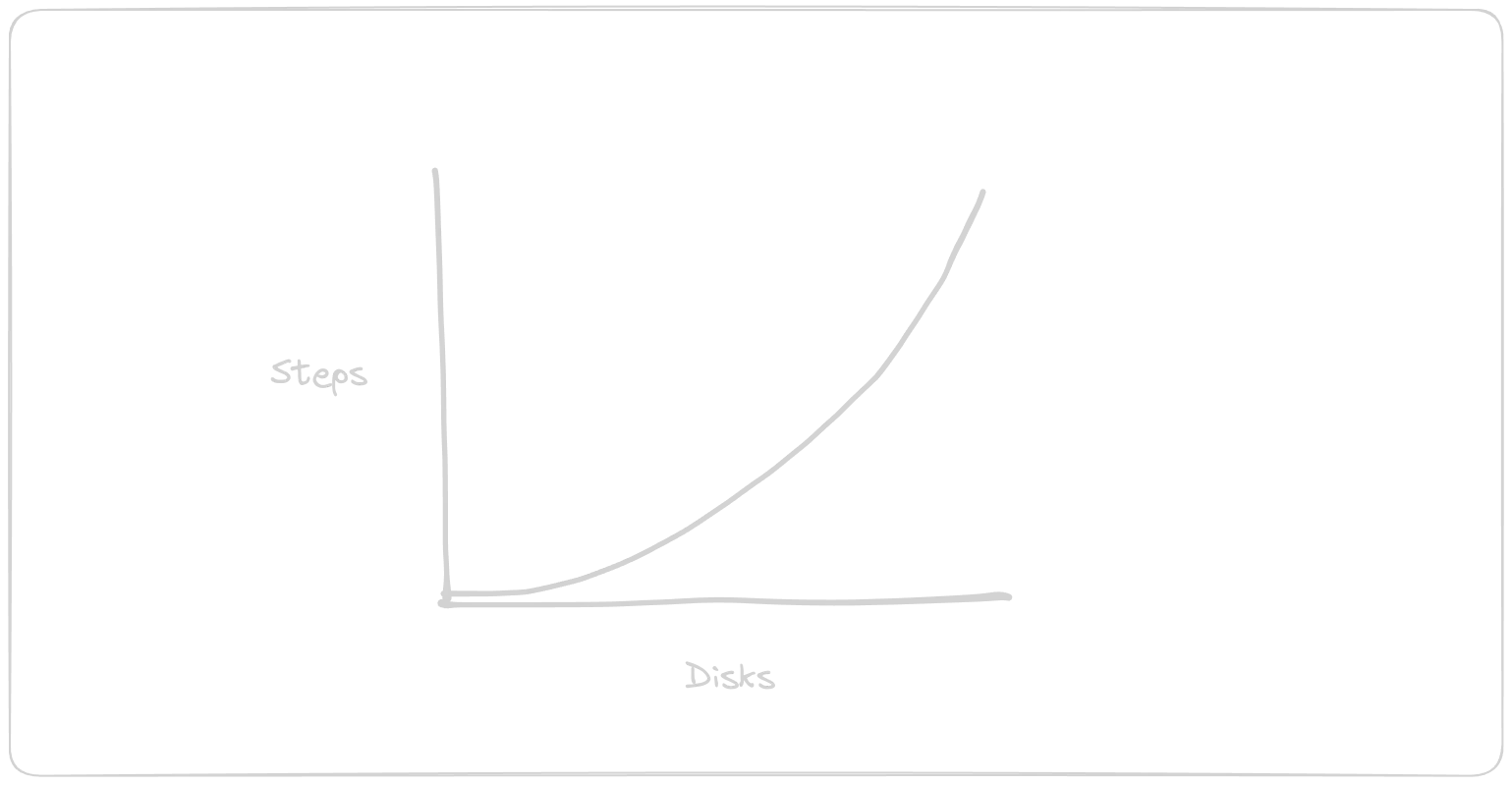
Below is a chart illustrating how the number of steps grows with the number of disks:

But here's the advantage of mathematical knowledge in this scenario:

If you ever need to create an algorithm that calculates the number of steps required to solve a Tower of Hanoi puzzle with any number of disks, you don't need to develop an entire solving algorithm. Instead, you can simply use the closed form that we discovered to determine the total number of moves needed. This reduces the algorithm's complexity from $O(2^n)$ to $O(1)$.

Certainly, you probably won't ever need to solve the Tower of Hanoi puzzle. However, trust me, this logical approach can be applied to many other situations in your daily work.

Conclusion

In this article, we explored the Tower of Hanoi puzzle from a mathematical perspective and used mathematics to determine its time complexity.

If you have any questions or feedback, please feel free to send me a message on LinkedIn. If you enjoyed the article, consider sharing it on social media so that more people can benefit from it!

References

• Book Concrete Mathematics, Second Edition, by Ronald L. Graham, Donald E. Knuth, and Oren Patashnik